导数和微分

基本概念

导数

$$ \left. \frac{\mathrm{d} y }{\mathrm{d} x} \right|{x=x{0}}=y’(x_0)=\lim_{h \to 0}\frac{f(x_0+h)-f(x_0)}{h} $$

单侧导数同理。

可导一定连续（相当于必然在该点有定义，是一个易忘的隐含条件）

微分需要稍微推一推。

微分

线性化

$$ \text{Assume f is differentiable at } x=a \text{. Denote} \newline \frac{f(x)-f(a)}{x-a} - f’(a) = \eta \newline \text{Then } \eta \text{ is small quantity near } x = a, \text{i.e.} \newline \lim_{x\to a}\eta = 0 \newline \ \text{We can write} \newline f(x) = f(a) + f’(a)(x-a)+\eta \cdot(x-a), \newline \text{So near } x=a\text{, we can make approximation} \newline L(x) = f(a) + f’(a)(x-a) \text{ with the error of } \eta (x-a) $$

就是函数上一点我们可以用切线进行一个近似，并且留下一个高次项的误差$\eta \cdot (x-a)$

上面的L便是f在a点的标准线性逼近。几何意义就是切线。

$L(x) = f(a) + f’(a)(x-a)$是在x=a处使用线性函数最好的逼近。下面我们进行一个证明。

这个思路给我的启发：设一个系数C来衡量“逼近的程度”。通过相同的论证我们还可以得出：

需要注意的是，逼近的意义在不同的场合中是不一样的。举一个经典的例子：圆的周长。

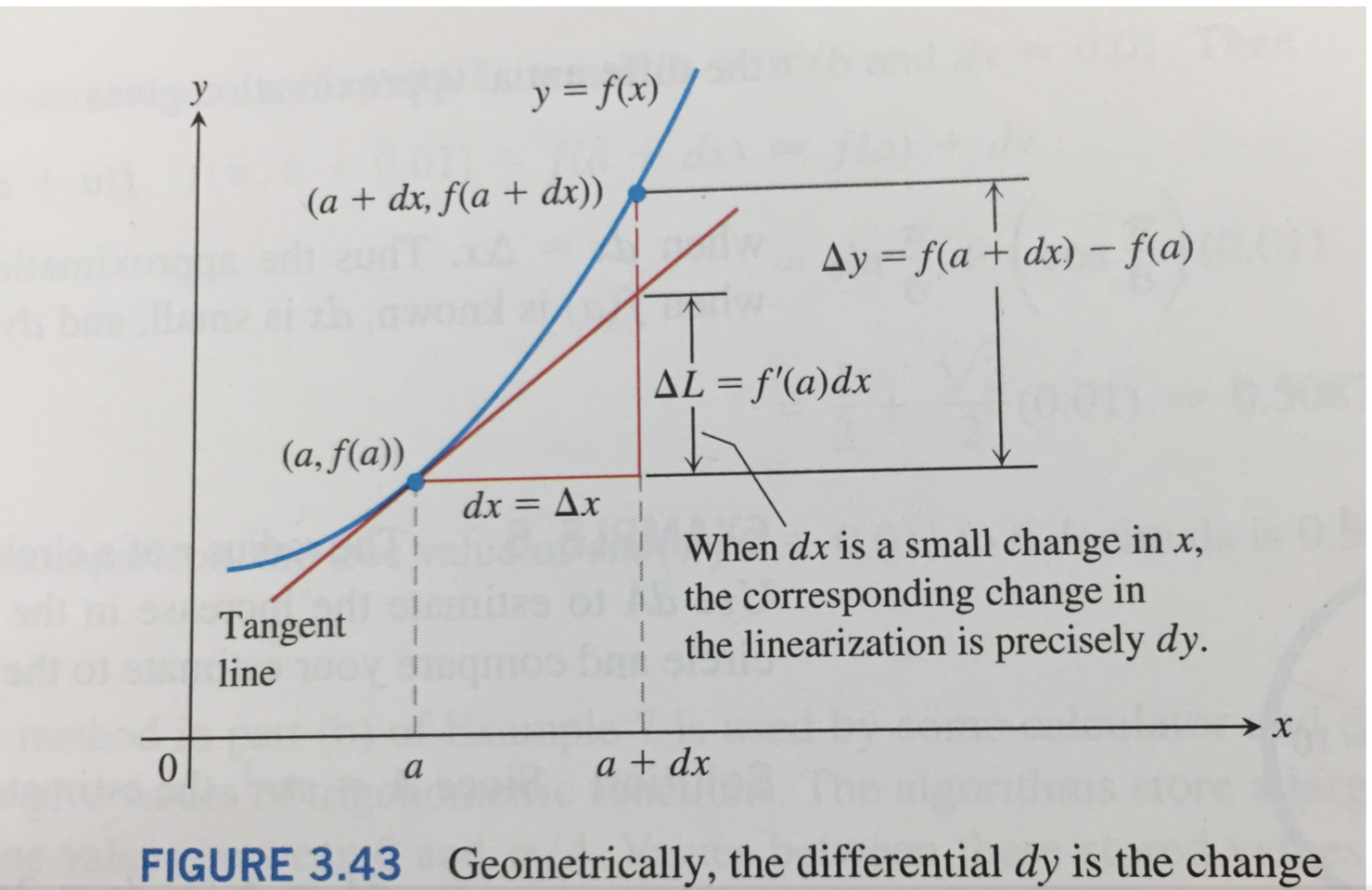
微分

$\Delta x和dx$没什么区别。$\Delta y$和$dy$还是有区别的。

$\Delta y = f’(a)\Delta x + \eta \Delta x$

$dy = f’(a)dx$

大O与小o

大O表示同阶，小o表示低阶，意味着括号内的东西接近某一个值的时候里面的东西比较小（非常小），具体拿来除一下看极限即可。