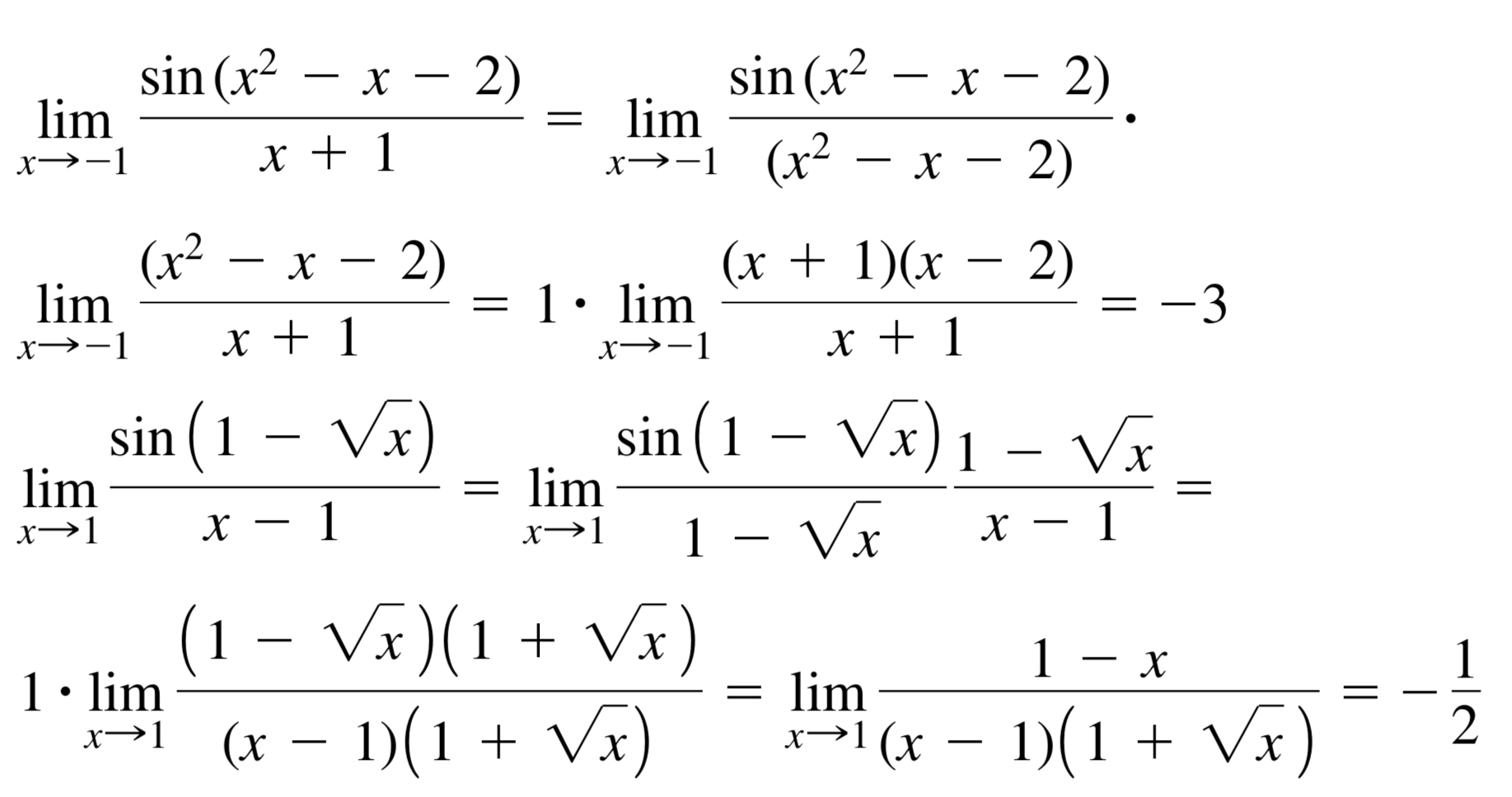极限与连续

法力无边的CJ的五个金手指

画画图、挖掘隐含条件、必要条件探路、正难则反、变结构

极限: $$ \text{we say} \lim_{x \to c}f(x) = L\quad \text { if},\quad \forall \epsilon>0, \quad \exists \delta>0 \ s.t. \newline \lvert f(x) - L \rvert < \delta \quad \text{ whenever } \quad 0< \lvert x-c\rvert<\delta $$ 连续： $$ \text{we say f is continuous at c} \quad \text {if},\quad \forall \epsilon>0, \quad \exists \delta>0 \ s.t. \newline \lvert f(x) - L \rvert < \delta \quad \text{ whenever } \quad \lvert x-c\rvert<\delta $$ 有几个地方需要特别整理：

• 恒等变形

• 放缩

• 定义的使用

  • 取$\epsilon$
  • 取$\delta$
  • 反证法

• 常见的可以使用的定理

• 小技巧

在极限与连续的相关题目中我们常用的几个方法：

正难则反、变结构，以及非常重要的定义的使用

恒等变形

处理次数的因式分解

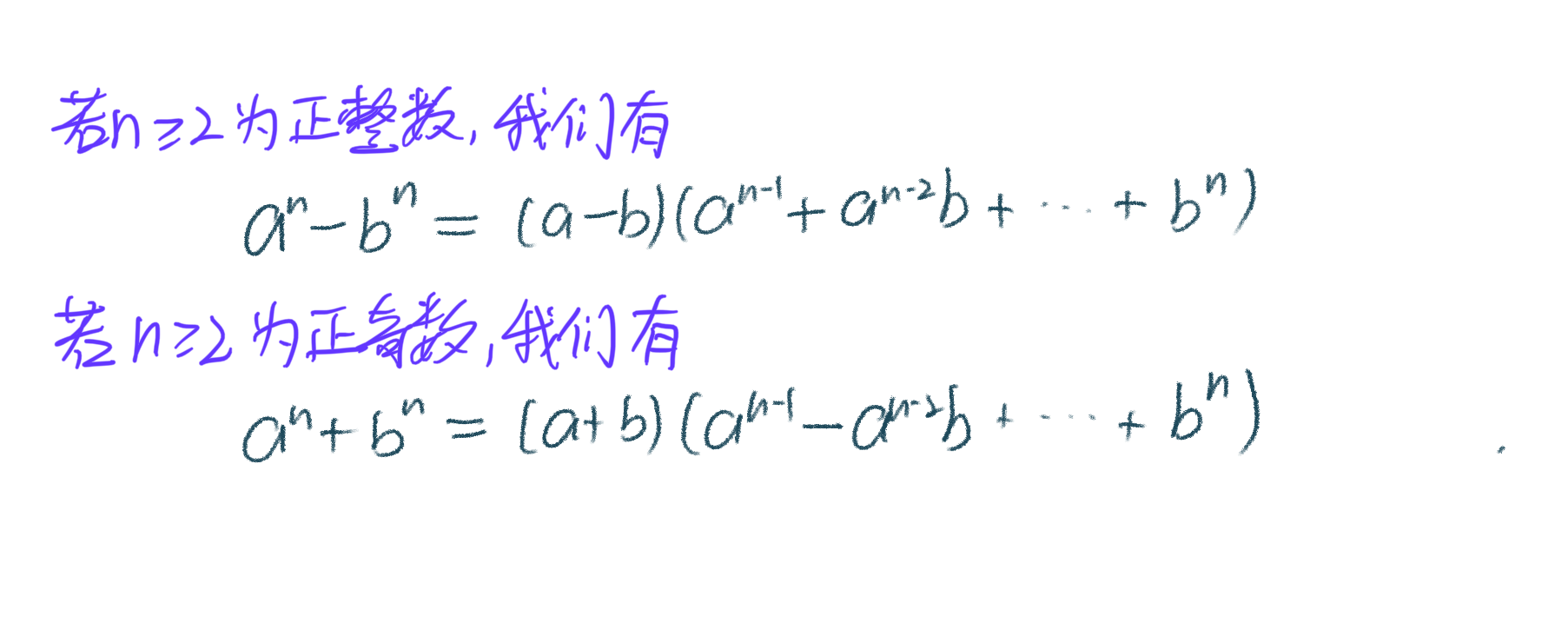
在此基础上，我们可以配合其他的因式分解技巧，我们也可以通过改变次数达到目标的效果。 $$ a=a^{n\times \frac1n}=a^{2\times\frac12} $$ 前一部分可以用来抵消一些根号项，后一部分可以实现偶数次方的次方和因式分解。

同时注意，这个公式逆用可以升次（root rule证明过程）

有理化

$$ \frac{1}{\sqrt{a}+\sqrt{b}} = \frac{\sqrt{a}-\sqrt{b}}{a-b} $$

可以是分子有理化也可以是分母有理化，根本目标是通过平方差公式来调整可以消掉的项。 有理化不追求一步到位，而是追求改变结构，也许是让一小部分可以约分，下面举一个例子：

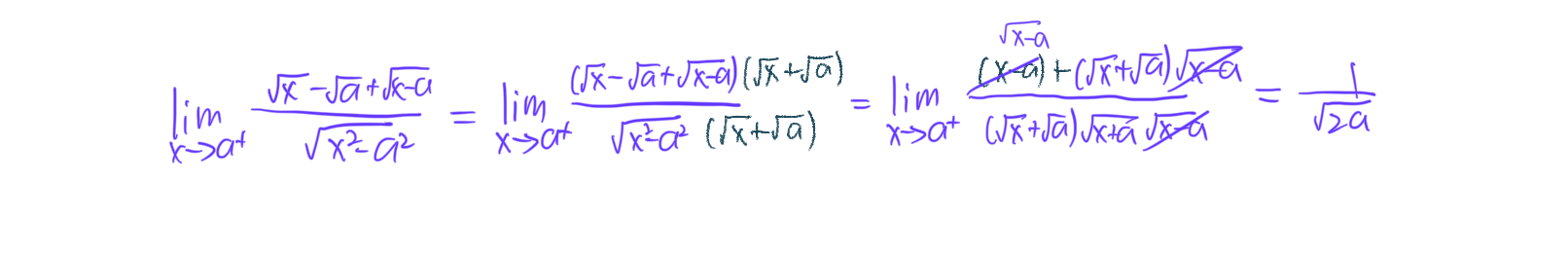
这里的有理化操作并没有非常有理化，但是有理化了一部分之后我们起到了约分的作用，非常的amazing。

拆分分子

$$ \frac{a+b}{c} = \frac{a}{c}+\frac{b}{c} $$

上面那一例“部分有理化也可以用这种方式解决（步骤多了几步，但是无伤大雅——自己最早想到的方法就是最好的）

加一项减一项

和定义、放缩一起使用，目标是把条件集中。例子见“做限制”

放缩

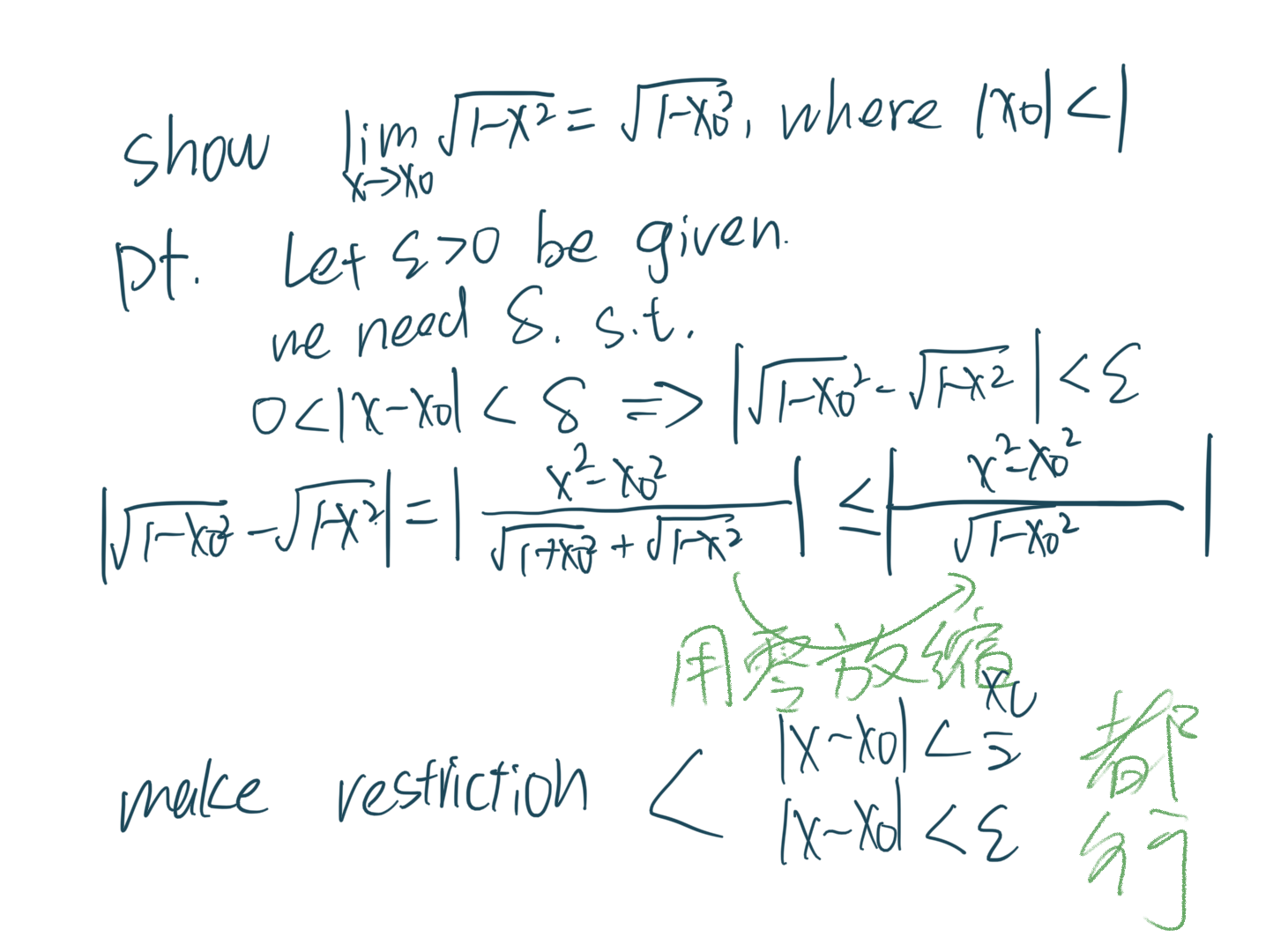
做限制

对于$\lim_{x \to c}f(x) = L$，所做的限制常常在$\displaystyle \lvert x - c \rvert$，并且在后续的放缩中一般不会把含有这个结构的东西全部放掉。我们最终的目标是只留下（并且解出）$\displaystyle \lvert x - c \rvert$的范围，我们要放掉的是（几乎）所有不含邮它的部分。下面来几个例子。

1、证明一个极限

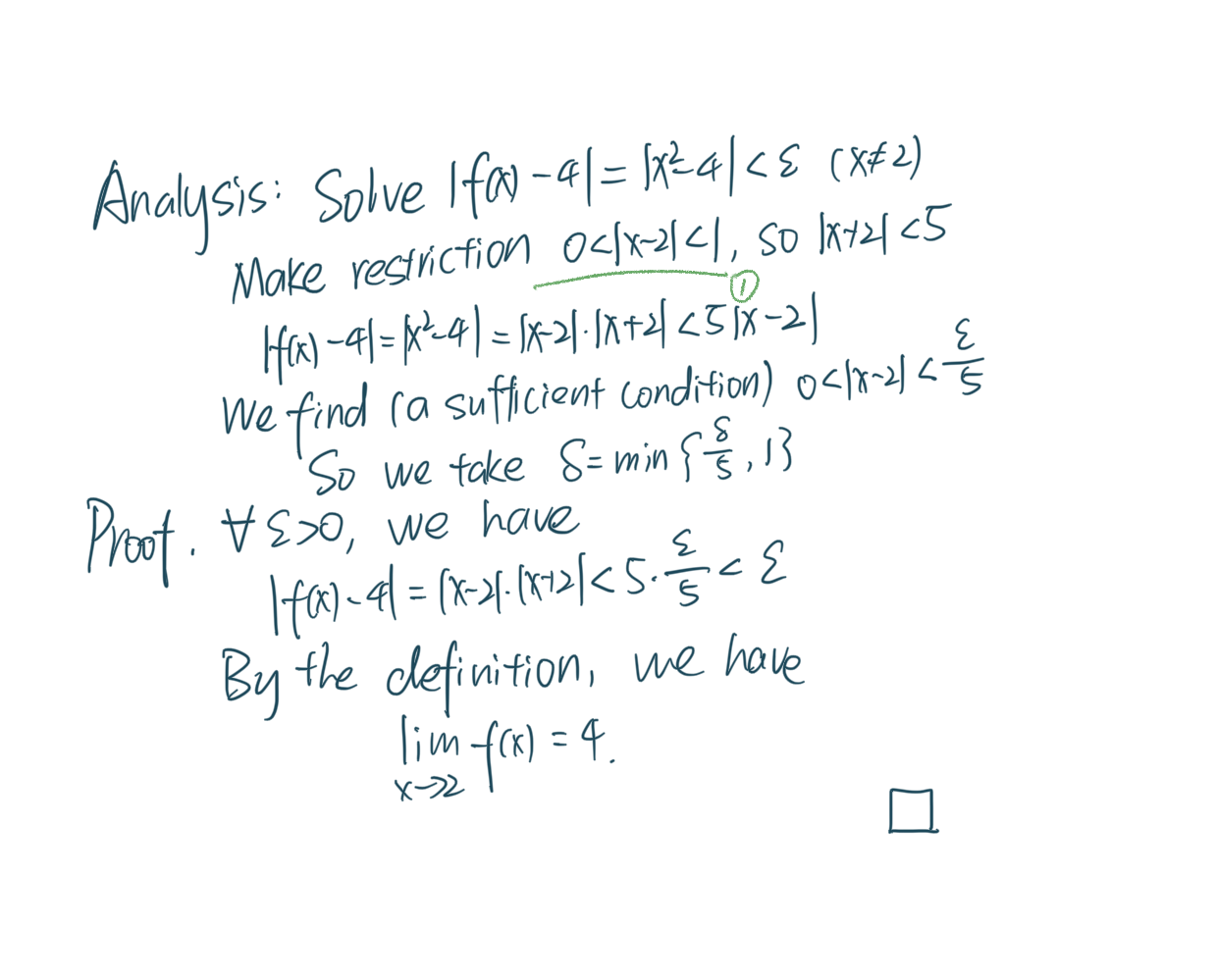
delta取两者之间的最小值是做限制的精髓。 做限制时你内心的想法：一般来说epsilon非常小。对于小于5的来说，限制成立；对于大于5的来说，取1就足够了。我们只需要一个必要条件。

2、证明极限运算的乘法法则

非常的有技巧啊，不得不加上一些说明：

• 加一项减一项，将相关的部分 ^{也就是x和x0，f（x）和L} 联系到一起，让定义可以使用。
• 其实这个make restriction和我们所说的不一样，其实是给$\epsilon$取了特定的值

二项式定理

二项式展开之后，你有两种选择

• 把所有项变成最大/最小的往里代
• 忽略不要的项

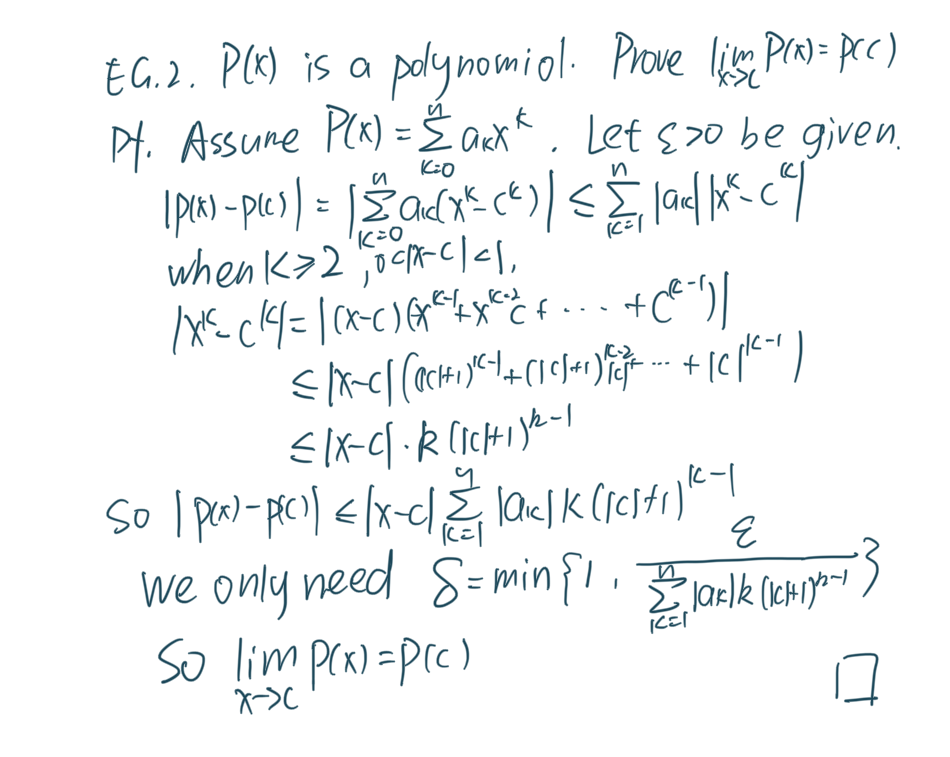
上面这个例子其实是做完了限制然后把所有东西往大里放，也就是第一种类型。

下面来一个“忽略不要的项”

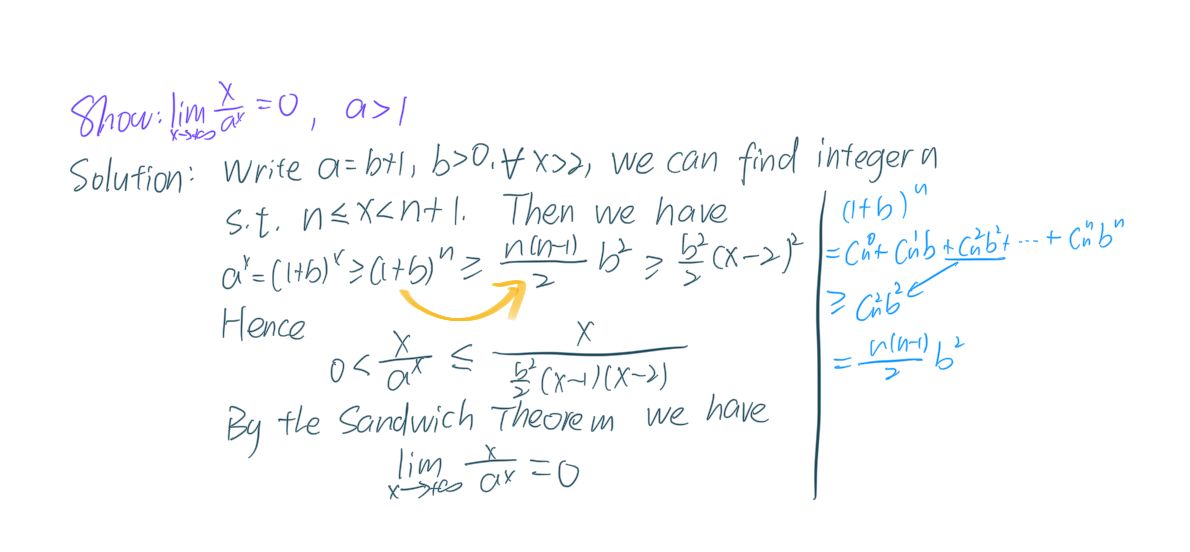
这里保留二次项是因为你想用两边夹的方法证极限。 这个不是最经典的放缩。最经典的是$(1+x)^n \geq 1+nx \quad(x>-1)$，实际上使用更为广泛。

将指数往下放我们也可以用这个式子。（n是整数，a大于1） $$ a^x=(1+b)^x \ge (1+b^n) \ge nb \ge (x-1)b $$

（绝对值）三角不等式

$$ \lvert \lvert a \rvert - \lvert b\rvert \rvert \le \lvert a+b \rvert \le \lvert a\rvert + \lvert b\rvert $$

大部分带绝对值的证明都可以用到。例子见“做限制”

次数的调节

与“无限”有关的极限求法离不开次数转化。在这里我们可以限制自变量和1的关系对指数直接操作。

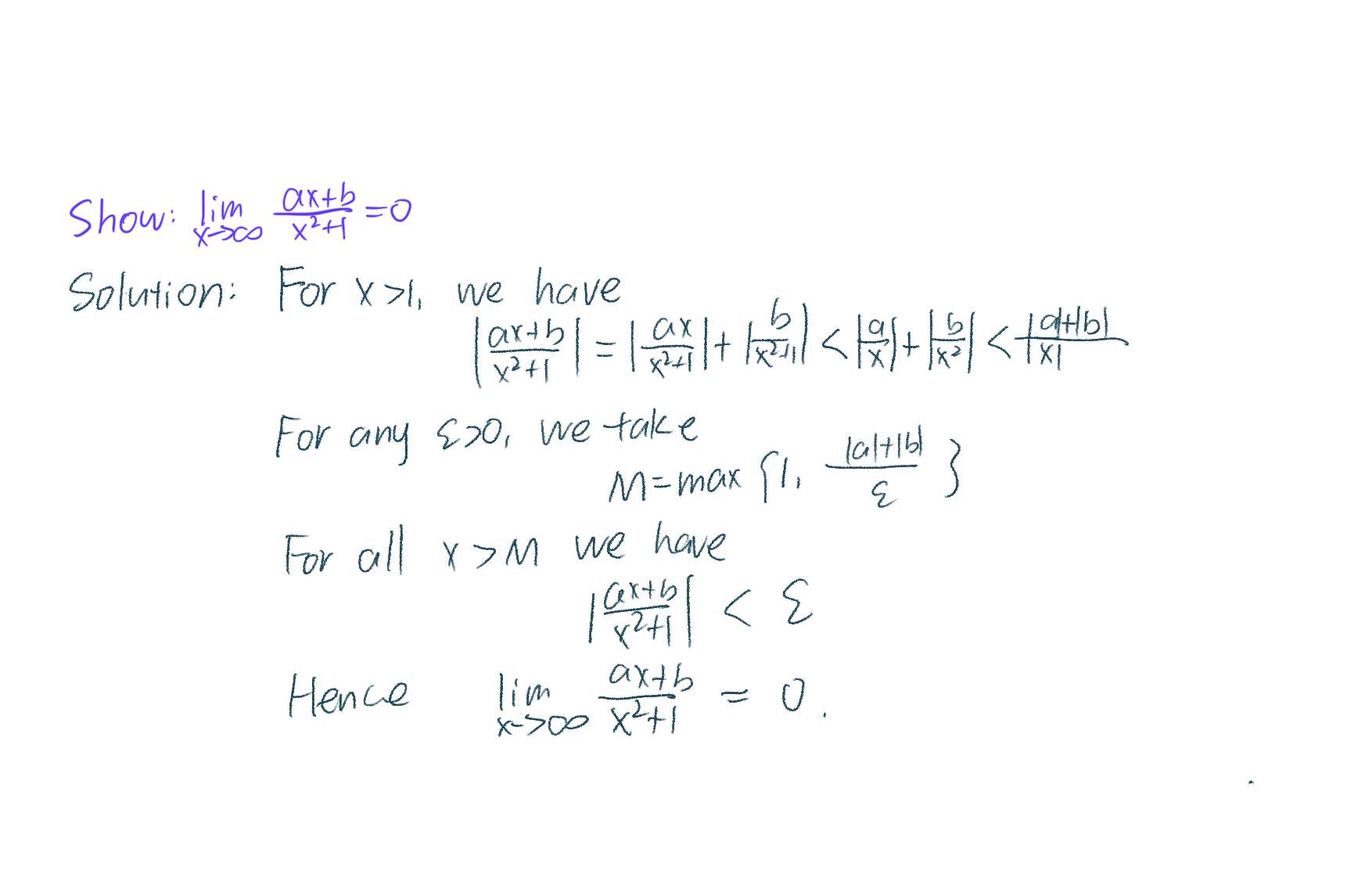
定义的使用

把定义写出来其实就差不多了

常见可用定理

两边夹（三明治定理）

保号性

在一个很小的delta内一定有同号的部分

保序性

$$ f(x)\leq g(x) \Rightarrow \lim_{x \to c}f(x) \leq \lim_{x \to c} g(x) $$

前提是定义域之类的条件全都要满足。

外面连续里面有极限

$$ \text{在外面连续里面有极限时} \newline \lim_{x \to c}g(f(x))=g({\lim_{x \to c}f(x)}) $$

仅仅是内外都有极限的话，如果保证在delta范围内不取到c就可以了

连续的另一种理解

$$ f \text{ is continuous at c} \Leftrightarrow \lim_{h \to 0} f(c+h)-f(c) = 0 $$

小技巧

避免分母为0

我们只要找一个必要条件。通过加一避免分母为0.在证明乘法法则中有使用到。 $$ \displaystyle \lvert L\rvert \cdot x <\lvert t\rvert \Leftarrow x < \frac{\lvert t\rvert}{\lvert L\rvert + 1} $$

不明显的有理化

看到根号想到有理化。哪怕根号下的已经足够繁杂。

$用\epsilon - \delta语言 证明 \displaystyle \lim_{x \to 1} \sqrt{\frac{7}{16x^2-9}}=1$

求极限时的变形

与无限有关的极限：分子分母同时除以最高次

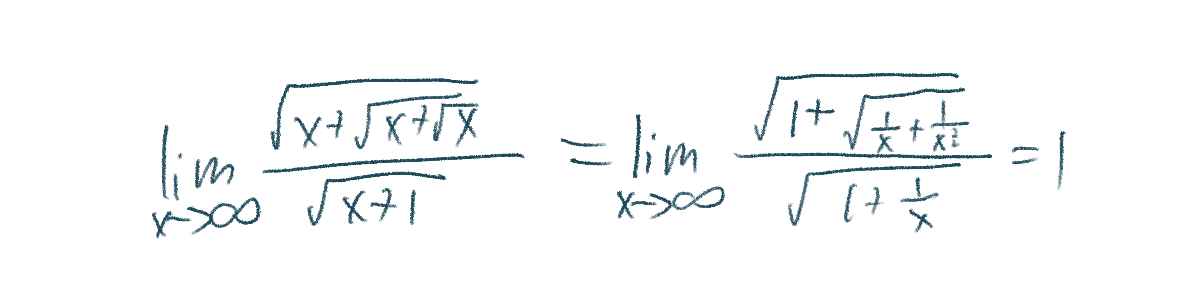
极限的运算可以添拆项来简化运算。